はじめに
KKTのT(投資)の学習を進める中で、CAPMの分野へ到達しました。CAPMと言われて正直、へっ?と思う方が大半かと思います。私もその一人でした。
今回は、初めての人でも分かりやすいように説明しますので是非最後まで読んで見てください。
CAPMとは?
CAPMとは、とあるリスク資産にどの程度のリスクが想定されるのか?そして、そのリスク量に対して、どの程度リターンを期待すればよいかを分析するモデルのことです。
実際のリターンを求める式
実際に、とあるリスク資産Aが存在する場合。期待リターンを求めるリターンの式は、以下のようになります。

上記のとおり、リスク資産Aの期待リターンは、市場全体のリターンと無リスク金利、そしてその資産の市場に対する感応度βによって、決定されます。
CAPMの定理
CAPMの基本概念の次に、定理について説明します。代表的な定理は2つあります。分離定理と期待リターンとβの関係です。
第1の定理:分離の定理
分離の定理とは、独自の投資判断をせず(市場に存在する最も効率的と考えられるリスク資産の組み合わせを選定する)、投資家の目的に応じてポートフォリオの調整を行うという考え方です。
資本市場線との関係
CAPMの第1の定理は、資本市場線にて表現することもできます。
以下のようになります。
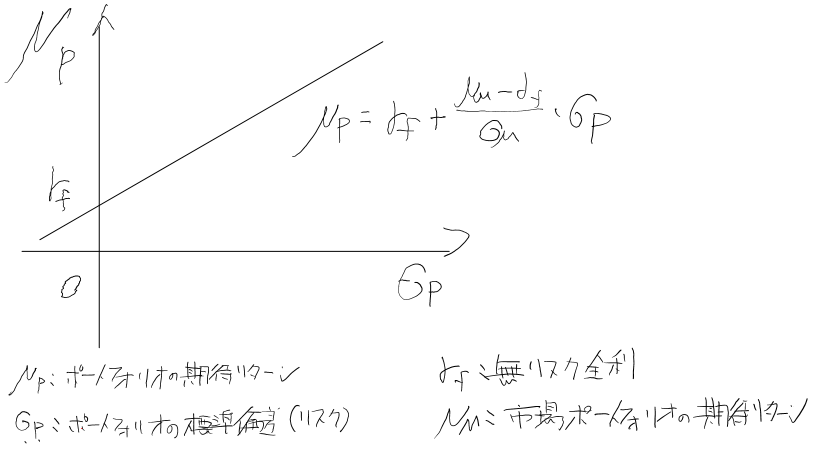
この線上においてであれば、ポートフォリオの調整を投資家の好みによって調整することができます。
第2の定理:期待リターンはβで決まる
つづいて、第2の定理ついてです。
第2の定理とは、リスク資産の期待リターンがどれだけ、市場全体に連動しているのかという内容です。いわゆる、リターンはリスクで決まるという考え方です。
このときのリターンの式です。CAPMのリターンの式と同じですね。

βの感覚論
以下に記載の通りですが、βの大小関係によって、リスクの大小は異なりますよね。

β(ベータ)・相関係数・標準偏差の関係式
CAPMでの、β(市場全体とのリスク尺度)と相関係数などの間には、実は関係式が成立しています。
リスク資産Aと市場とのリスク尺度βの場合は、以下のようになります。
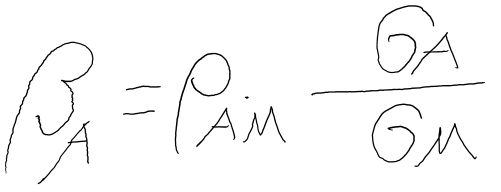
記載するまでもないかと思いますが、各変数は以下のような定義です。

相関係数 =の形にすれば、以下のような式になります。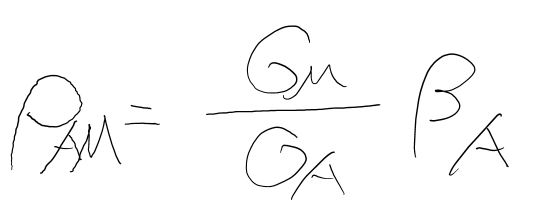
ジェンセンのα
ジェンセンのαとは、CAPMで予測されるリターンと実際のリターンの差分のことです。
以下、リスク資産iとしたときの例です。

共分散・シャープ比の関係
CAPMの重要な構成要素であるベータや相関係数の説明に加えて、リスク評価に関連する他の統計量との関係についても整理を行います。
非市場リターンの独立性と共分散
CAPMにおいては、各資産の非市場リスク部分(以下画像のσe部分)が互いに独立である場合、共分散は0となります。
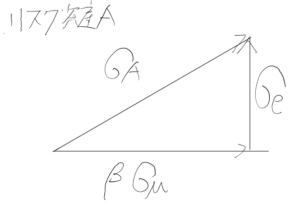
ここでいう(独立)とは、
ある資産Aに関する情報や要因が、他の資産Bの価格やリターンに一切影響を与えないことを意味します。確率変数として独立であることということは、同時にその共分散がゼロであることを意味します。つまり、「リスク資産Aの変動がリスク資産Bの変動に影響を与えない」ということです。

この仮定により、特有リスクは分散投資で打ち消され、市場リスク(ベータ)のが分析対象になります。
※特有リスク=非市場リスクが消えます。
シャープ比との関係
CAPMでは、効率的ポートフォリオがシャープ比を最大化するとされます。

再度の掲載にはなりますが、CAPMを資本市場線において表すと以下の通りになります。

つまり、「リスク1単位あたりにどれだけ超過リターンがあるか」を示す尺度であり、資本市場線の傾きでもあります。
分散の定義について、再確認
分散とは、リターンが平均からどの程度ばらつくかどうかを示す指標のことです。
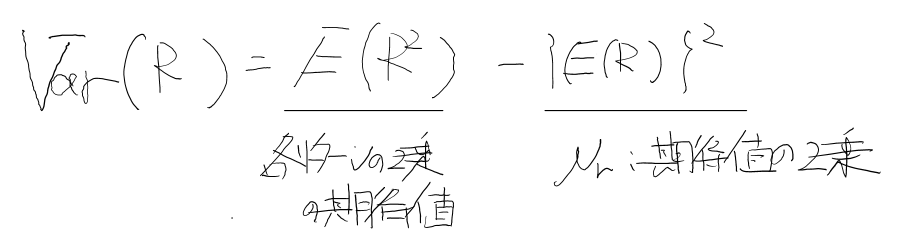
各項目はなぜか?
①:各リターンを2乗してから平均を取るのは、ばらつきを大きく反映するためです。②:また、リターンの平均を最初に算出し、2乗をするのは、中心的な水準(平均)を算出するためです。
結果、① ー ②を行うことで、リターンのばらつきを(リスク)だけを抽出することができます。
例題
とあるリスク資産が、ある2つ期間において、10%とー10%のリターンを出す場合、リターンとリスク及びそれに関わる、リスクはどのようになるかについて考えてみます。
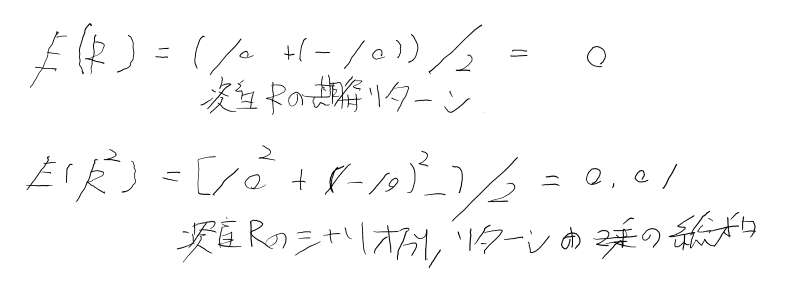
よって、シナリオ別のリターンの2乗の総和ー期待値の2乗のため、この資産のリスクは0.01となります。
関連
リスク資産単体のリスクに対して、ポートフォリオ(複数から構成される)資産のリスクは負う評価されるのかについて、併せて説明します。
以下、公式で説明することができます。
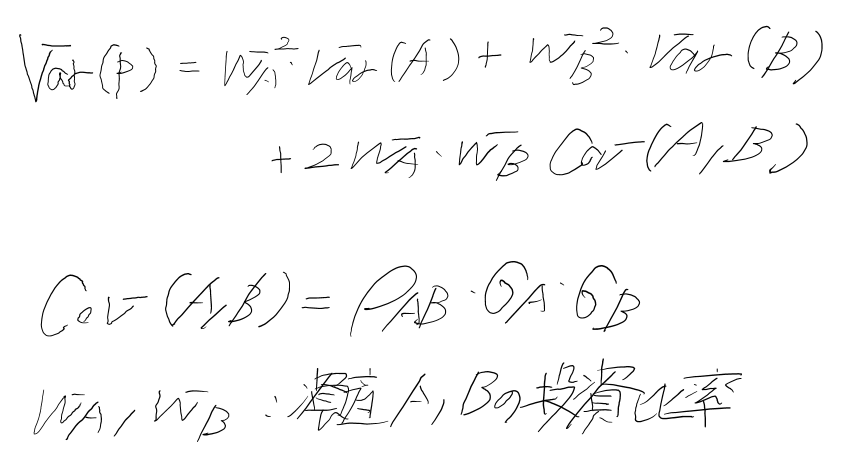
CAPMの世界では、非市場リスクの共分散がゼロであるという仮定のもと、分散は主に市場との関係(β)で構成されます。
まとめ
CAPMは、シンプルな理論であり、投資理論や運用評価の土台となる理論で株主資本コストやファンドのパフォーマンス評価や投資案件の評価、公共投資・インフラ評価への応用に称されます。
分離定理(第1の定理)、第2の定理、そしてα、β、シャープ比といった概念から投資成果を評価します。実務においても幅広く活用されているため、CAPMを理解することはリスクとリターンのバランス調整に理論的に根拠をもつことができます。

